Quadrilaterals Explained: Types, Formulas & Theorems (2025 Guide)
Introduction
In our daily lives, we come across several four-sided 2D figures called quadrilaterals. Have you ever wondered what makes every quadrilateral unique in its own term? Every four-sided figure has its own properties and formulas that distinguish them from other polygons.
According to geometry, the sum of the internal angles of a quadrilateral is 360 degrees. A quadrilateral is a closed shape with 4 sides. So, we have come up with a blog that defines and explains the properties of five types of quadrilaterals namely:
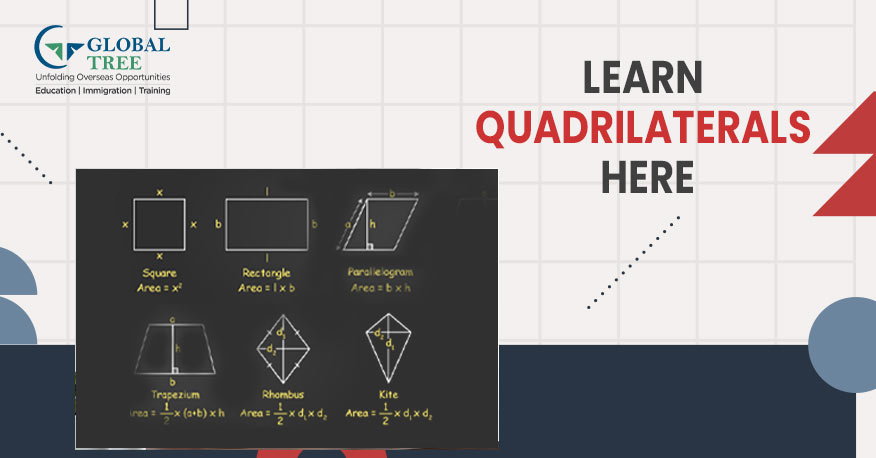
The five types of quadrilaterals are:
- Rectangle
- Square
- Parallelogram
- Rhombus
- Trapezium
What are the properties of the quadrilaterals?
The quadrilateral is a four-sided figure and all the internal angles add up to give 360 degrees. Thus, adding ∠A + ∠B + ∠C + ∠D gives you 360°. While preparing for exams like GMAT, the basics of the subject play a key role in improving the GMAT score.
| Properties of quadrilaterals | Rectangle | Square | Parallelogram | Rhombus | Trapezium |
|---|---|---|---|---|---|
|
All Sides are equal |
No |
Yes |
No |
Yes |
No |
|
Opposite Sides are equal |
Yes |
Yes |
Yes |
Yes |
No |
|
Opposite Sides are parallel |
Yes |
Yes |
Yes |
Yes |
Yes |
|
All angles are equal |
Yes |
Yes |
No |
No |
No |
|
Opposite angles are equal |
Yes |
Yes |
Yes |
Yes |
No |
|
The sum of two adjacent angles is 180 |
Yes |
Yes |
Yes |
Yes |
No |
|
Bisect each other |
Yes |
Yes |
Yes |
Yes |
No |
|
Bisect perpendicularly |
No |
Yes |
No |
Yes |
No |
Rectangle
The rectangle is a quadrilateral which has four right angles. The opposite sides of a rectangle are equal and parallel, and the diagonals bisect each other. Every angle in a rectangle is 90°.
(360°/4 = 90°).
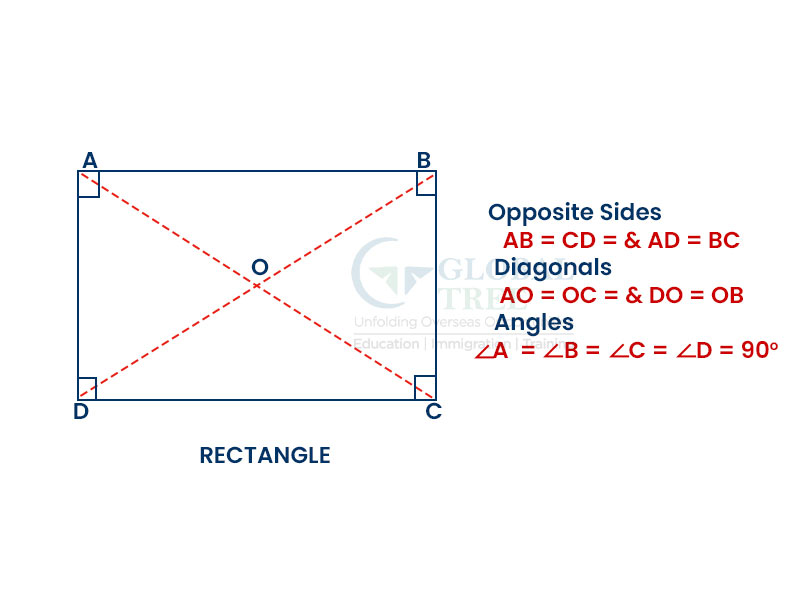
The Properties of a rectangle are:
- Each angle is 90°
- The opposite sides are equal and parallel
- Diagonals in a rectangle bisect each other
(Read More: STEM Courses to Study Abroad for Indian Students)
Formula: Area ad Perimeter of a rectangle
The length of the rectangle is L and the breadth of the rectangle is B.
Then, the Area of a rectangle= Length* Breadth
The perimeter of the rectangle= 2*(L+B)
Square
A square is a quadrilateral that has four equal angles and sides. Just like the rectangle, every angle in a square is 90° each.
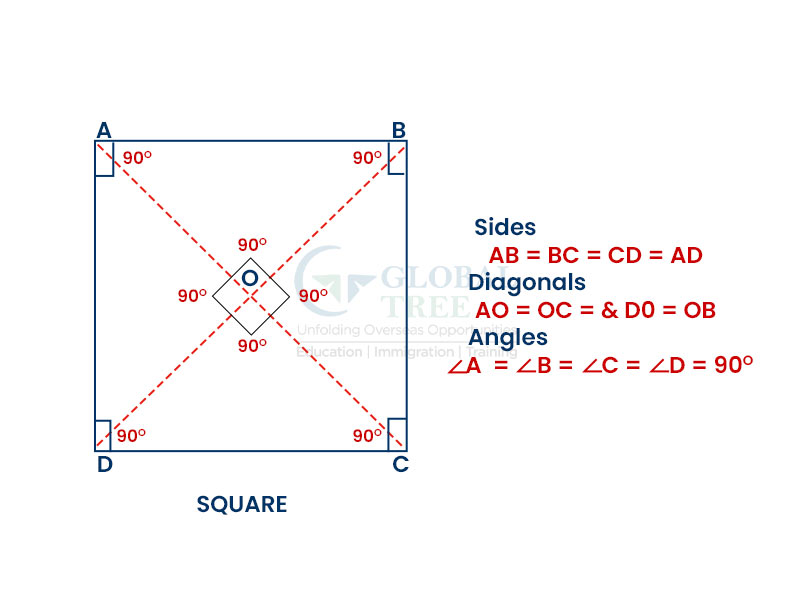
The three properties of a Square are:
- Every angle in a square is 90°
- All sides are equal and parallel to each other in a square
- Diagonals in a square bisect each other perpendicularly.
Formula –
Consider ‘a’ as the side of a square then,
The area of the square is given as a × a = a²
The perimeter of the square is given as 2 × (a + a) = 4a
You might have learned the topic of Quadrilaterals at your school level. Most of you may not remember the concepts gained that are most useful for exams like GRE. Instead, opt for GRE coaching nearby for professional training.
Parallelogram
A parallelogram is a quadrilateral and it has two pairs of parallel sides. The opposite angles are equal and the diagonals bisect each other in a parallelogram.
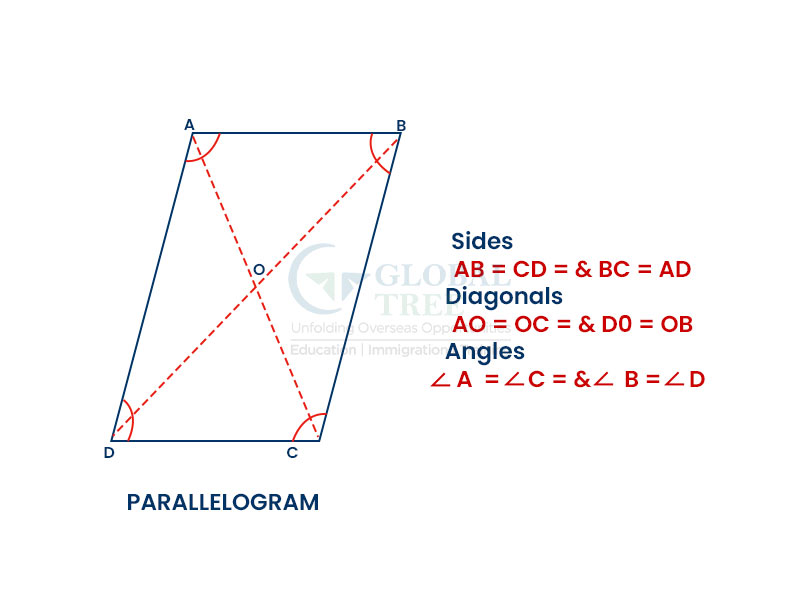
Properties of parallelogram
The opposite sides are equal and parallel
The diagonals in a parallelogram are equal and parallel
The sum of any two adjacent angles in a parallelogram is 180°
Consider the length of a parallelogram as ‘l’, breadth as ‘b’, and height as ‘h’ then:
The perimeter of parallelogram= 2*(l+ b)
Area of the parallelogram= l*h
(Read More: How to score high on the GRE Quant Section?)
Rhombus
The Rhombus has four sides. The four sides are equal in length. The opposite sides are said to be parallel to each other. Rhombus is also designated as a diamond.
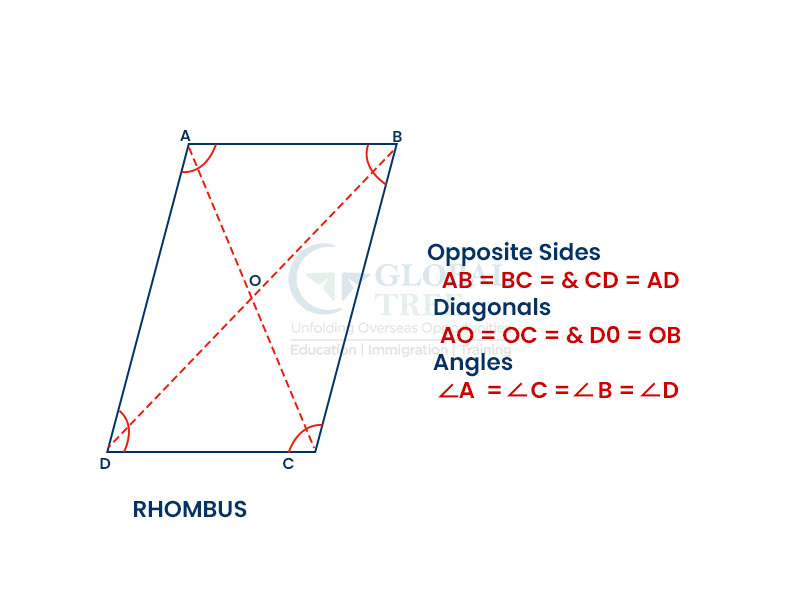
Properties of rhombus
The Opposite angles are equal in a Rhombus
All sides are equal. A rhombus has opposite sides that are parallel.
A rhombus has diagonals that bisect each other at 90 degrees.
The Sum of any two adjacent angles is 180° in a rhombus.
Formula– If ‘a’ is the side of a rhombus, then the perimeter of a rhombus= 4a
d1, d2 are the lengths of two diagonals in a rhombus, then the area of a rhombus= ½ × d1 × d2
Trapezium
The trapezium is also called a Trapezoid and it has only one pair of parallel sides. The parallel sides are designated as bases and the other two sides as lateral sides.
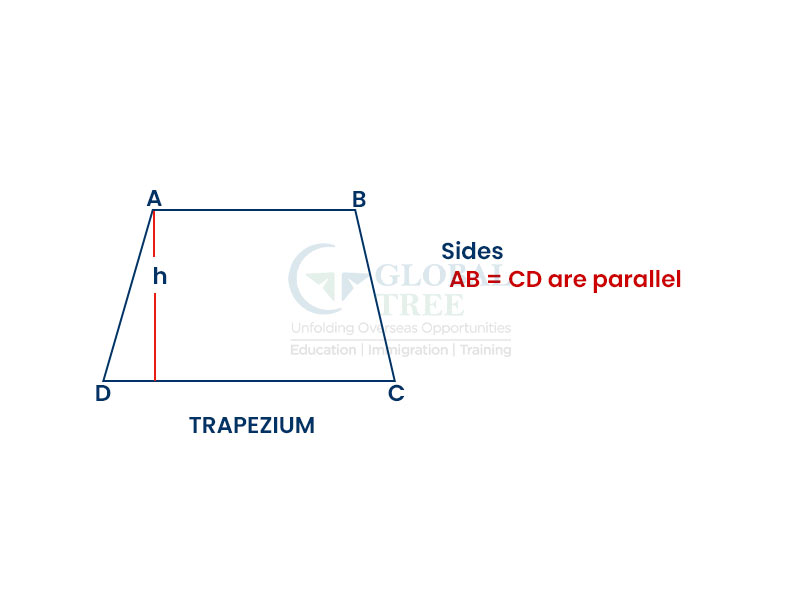
Properties of trapezium
Only one pair of opposite sides are parallel to each other in a trapezium.
The height of the trapezium in the above picture is given as ‘h&rsquo.
The perimeter of the trapezium= AB + BC + CD + DA
Area of the trapezium = ½ × (Sum of lengths of parallel sides) × h = ½ × (AB + CD) × h
(Read More: 5 tips to boost your GRE score)
The most important formulas:
The below table represents the formulas for the area and perimeter of different types of quadrilaterals:
| Quadrilateral formulas | Rectangle | Square | Parallelogram | Rhombus | Trapezium |
|---|---|---|---|---|---|
|
Area |
l × b |
a² |
l × h |
½ × d1 × d2 |
½ × (Sum of parallel sides) × height |
|
Perimeter |
2 × (l + b) |
4a |
2 × (l + b) |
4a |
The sum of all the sides |
GMAT Quadrilaterals Practice Question 1
1) Venu has planned to build a fence around his rectangular garden that has a length of 10 meters and a breadth of 15 meters. How many meters of the fence is required to fence the entire garden?
- 20 meters
- 25 meters
- 30 meters
- 40 meters
- 50 meters
Solution:
Step 1: The length of the rectangular garden= 10 meters
The width of the rectangular garden= 15 meters
He wants to build a fence around the rectangular garden.
Step 2: To find the length of the fence required to build around the entire garden.
Step 3: Remember that fence can only be built around the outer section of the garden.
The total length of the fence= Sum of the lengths of all sides of the garden
Since the given garden is in rectangular shape, the sum of the length of the sides=perimeter of the garden.
Perimeter = 2 × (10 + 15) = 50 metres
Therefore, the required length is 50 meters. Thereby, option E is the correct option.
GMAT Quadrilaterals Practice Question 2
2) Stella wants to paint a rectangular-shaped wall in her bedroom. The cost is $1.5 per square meter to paint the wall. If the length of the wall is 25 meters and the width of the wall is 18 meters, then what is the total cost of painting the wall?
- $ 300
- $ 350
- $ 450
- $ 600
- $ 675
Solution
Step 1: Given that Stella wants to paint her room
The Length of the wall is 25 meters long and the width of the wall is 18 meters.
The cost to paint the wall = $1.5 per square meter.
Step 2: To find the total cost to paint the rectangular-shaped wall.
To find the total cost to paint the wall in square meters, follow the below steps:
- Find the total area of the wall in square meters
- Multiply it by the required cost to paint the 1 square meter of the wall
- Thereby, we can find the price. A wall is painted across its entire area.
Area of the wall = length × Breadth
18 metres*25 metres = 450 square metres
Total cost to paint the wall = 450 × $1.5 per square meter = $675
Therefore, the correct answer is option E.









